🥰 Projects 🥰

Evolution Meets Diffusion: Efficient Neural Architecture Generation

Introduction

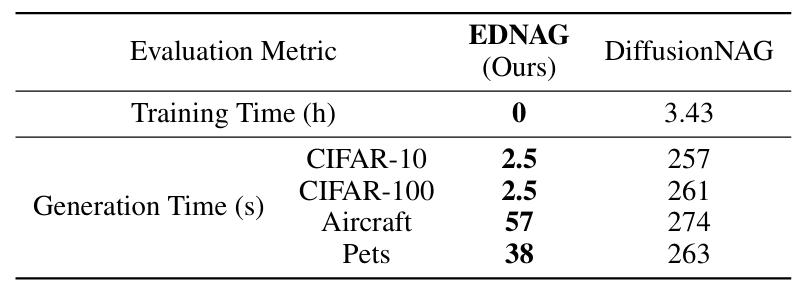
Neural Architecture Search (NAS) has gained widespread attention for its transformative potential in deep learning model design. However, the vast and complex search space of NAS leads to significant computational and time costs. Neural Architecture Generation (NAG) addresses this by reframing NAS as a generation problem, enabling the precise generation of optimal architectures for specific tasks. Despite its promise, mainstream methods like diffusion models face limitations in global search capabilities and are still hindered by high computational and time demands. To overcome these challenges, we propose Evolutionary Diffusion-based Neural Architecture Generation (EDNAG), a novel approach that achieves efficient and training-free architecture generation. EDNAG leverages evolutionary algorithms to simulate the denoising process in diffusion models, using fitness to guide the transition from random Gaussian distributions to optimal architecture distributions. This approach combines the strengths of evolutionary strategies and diffusion models, enabling rapid and effective architecture generation. Extensive experiments demonstrate that EDNAG achieves state-of-the-art (SOTA) performance in architecture optimization, with an improvement in accuracy of up to 10.45%. Furthermore, it eliminates the need for time-consuming training and boosts inference speed by an average of 50×, showcasing its exceptional efficiency and effectiveness.

Contributions

• Propose a novel Evolutionary Diffusion-based framework for Neural Architecture Generation (EDNAG), which simulates the denoising process in diffusion models within an evolutionary paradigm.
• Introduce a Fitness-guided Denoising (FD) strategy, which utilizes fitness instead of trained networks to generate offspring architecture samples from previous ones, achieving the first network-free neural architecture generation approach.
• Conduct extensive experiments to demonstrate the SOTA performance of EDNAG in architecture generation with significantly fewer computational resources, as well as its outstanding adaptability and transferability.

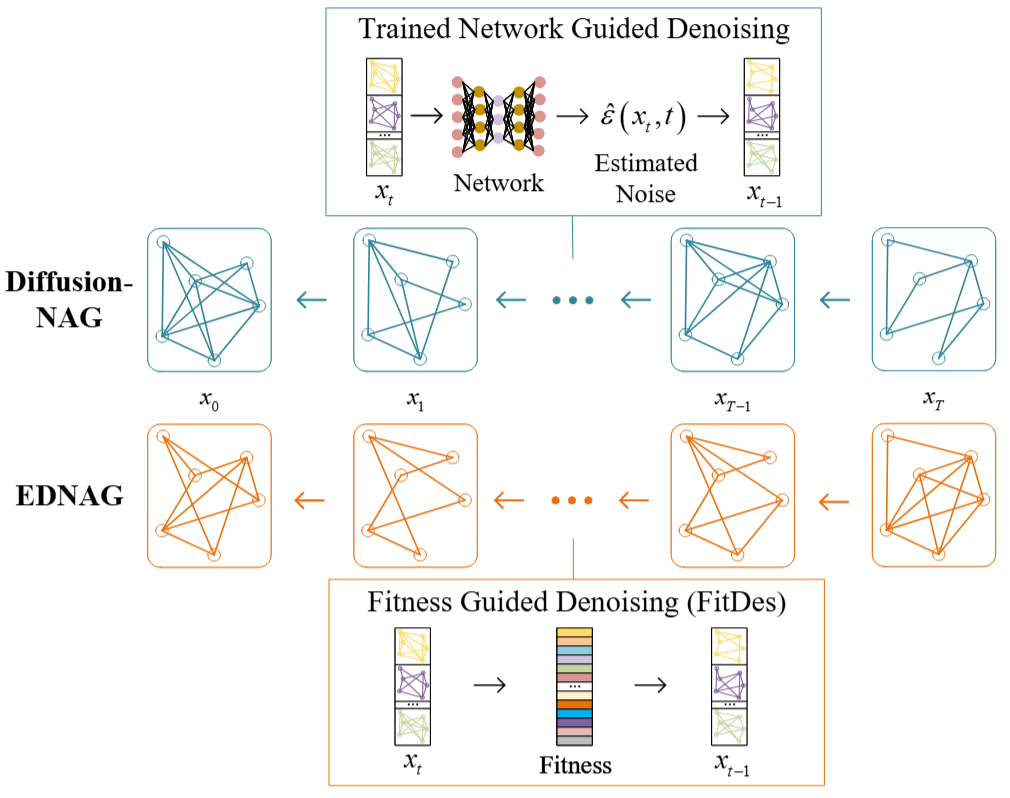
Methods

The core innovation of EDNAG is its simultaneous enhancement of both efficiency and generation quality. Specifically, we introduce evolutionary algorithms to simulate the denoising process within diffusion models. Furthermore, we propose a Fitness-guided Denoising (FD) strategy, which generates new architectures from previous ones at each denoising iteration. Each newly generated architecture can be represented as a weighted summation of prior samples, where superior architectures are assigned higher weights and thus exert greater influence. As a result, architecture samples progressively evolve toward high-fitness subspaces through multiple FD-guided denoising iterations, ultimately yielding high-performing and globally optimal neural architectures.
In particular, EDNAG leverages a neural predictor for task-specific neural architecture generation, serving as a dataset-aware fitness evaluator that guides the conditional generation process within the FD strategy. Notably, the FD strategy removes the reliance on score networks used in traditional diffusion models during the denoising process, enabling network-free neural architecture generation and substantially improving generation efficiency.

Derivations

For diffusion models like DDIM, in the forward process, we blend data with Gaussian noise, perturbing the original data x0 to the final diffused data xT as Eq (1).

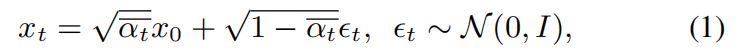
In the reverse process, DDIM removes the noise from the randomly initialized data step by step, which is represented as Eq (2).
Traditional DDIM leverages a neural network ϵθ to predict perturbed noise ϵˆθ (xt, t) at time step t, guiding the denoising process. By iteratively repeating this denoising process in Eq (2), DDIM progressively generates the final samples.

For each denoising iteration, let xˆ0 denotes the predicted x0 in Eq (2).

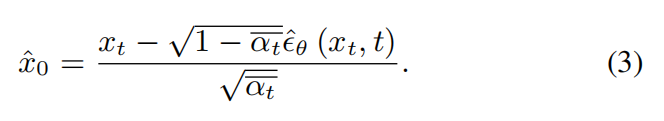
With Eq (3), the denoising process can be transformed into Eq (4).

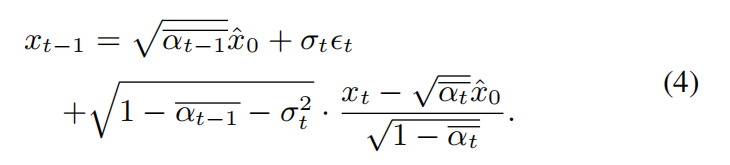
Therefore, to perform the denoising process from xt to xt-1, it is only necessary to determine the predicted optimal architectures xˆ0 based on xt, αt and t.
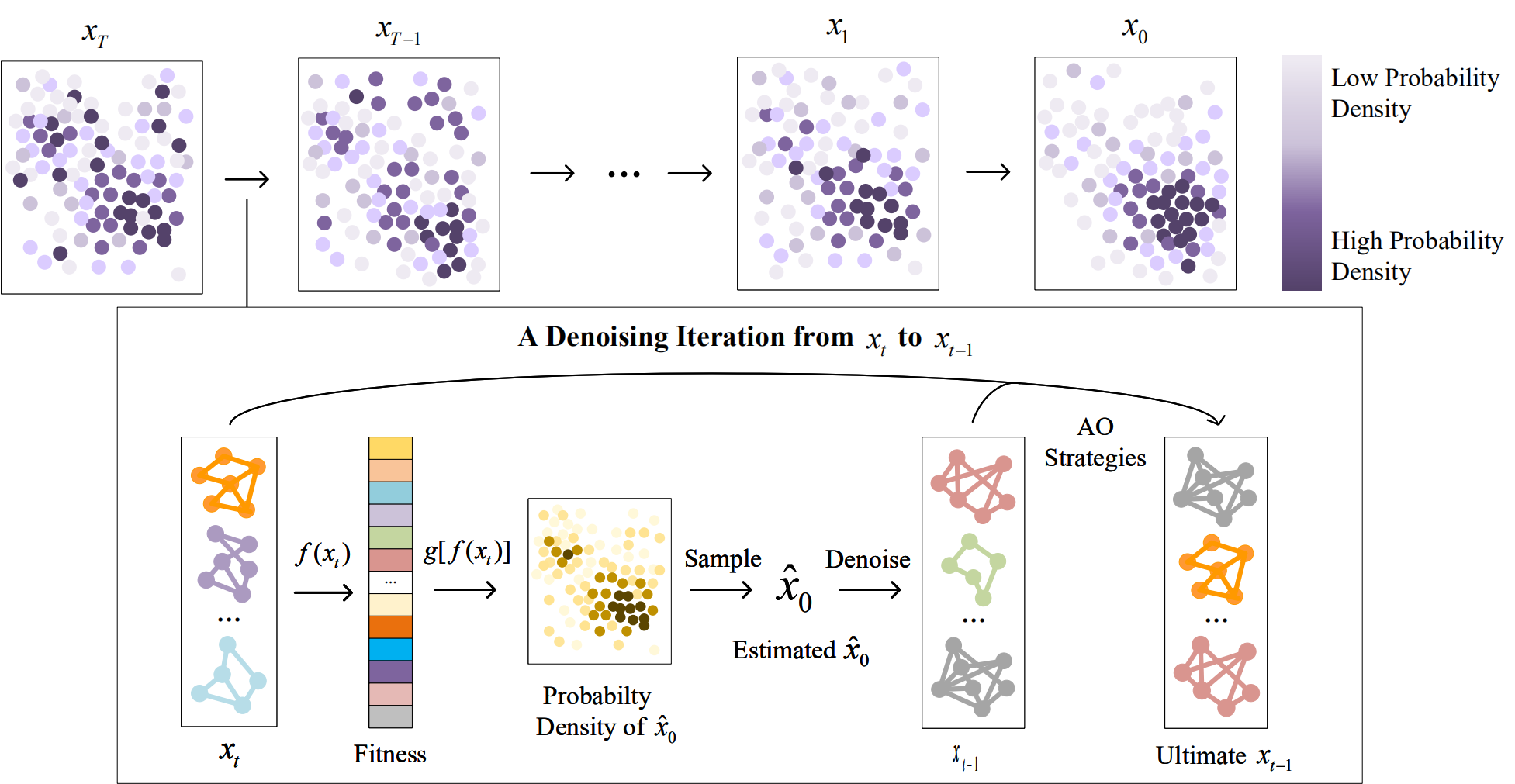
To estimate xˆ0, Fitness-guided Denoising (FD) strategy maps the distribution of xt to the distribution of xˆ0 with fitness guidance. Specifically, we view the denoising process of DDIM as the evolutionary process of GAs, both transforming samples from an initial random Gaussian distribution to an ultimate optimal distribution progressively [47]. We consider that individuals with higher fitness are more likely to be retained during evolution, resulting in a higher probability of appearing in the final samples xˆ0. Therefore, higher fitness corresponds to a higher probability density in xˆ0. We model this relationship as a mapping function g(x), which maps the fitness f(xt) of xt to the probability density p(ˆx0) of xˆ0:

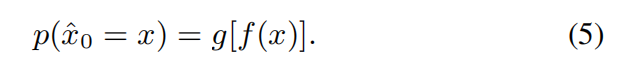
Hence, the optimal architectures xˆ0 can be estimated from the samples xt at time step t and their fitness f(xt), as detailed in Eq (6).

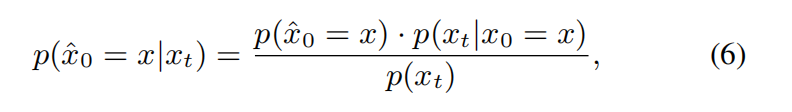
where p(xt|x0 = x)is s derived from the diffusion process described by Eq (1), as shown in Eq (7).

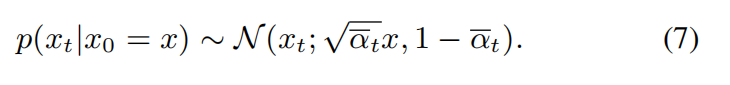
We further define xt as the previous samples consisting of N architectures, where xt = [x1t , x2t, . . . , xNt]. Combining Eq (6) and (7), xˆ0 can be estimated as follows.

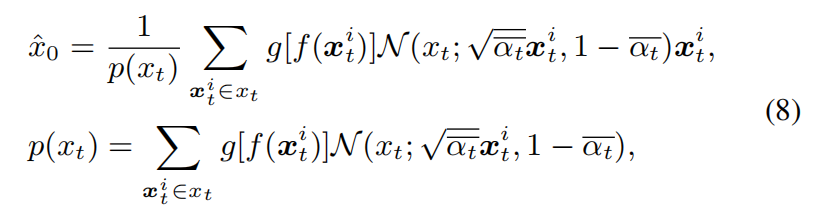
where p(xt) actually serves as a regularization term. In fact, xˆ0 can be regarded as the weighted summation of each neural architecture xt^i in samples xt, where architectures with higher fitness have a greater influence on xˆ0. Finally, with Eq (4) and (8), we can denoise from xt to xt-1 as Eq (9).

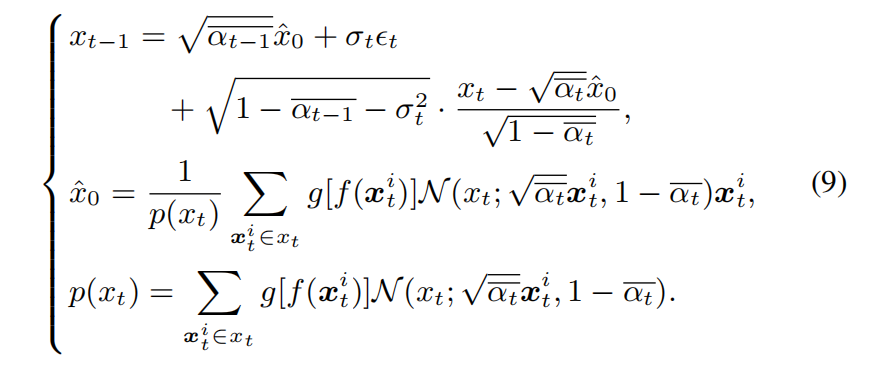
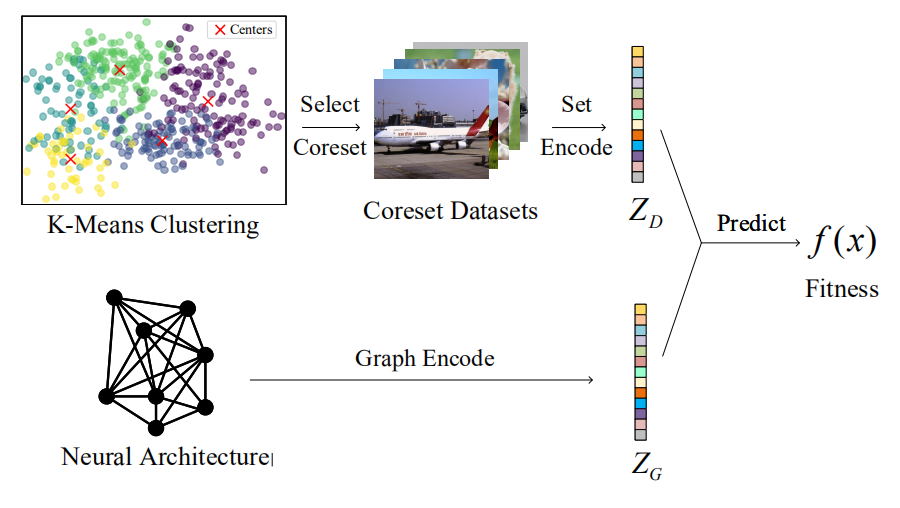
For fitness evaluation, we utilize a neural predictor to evaluate the fitness of each architecture. The entire process is detailed in the following figure.

Our predictor comprises coreset selection, dataset encoding, architecture encoding, and accuracy prediction modules, which is detailed in the following figure.

Experiments

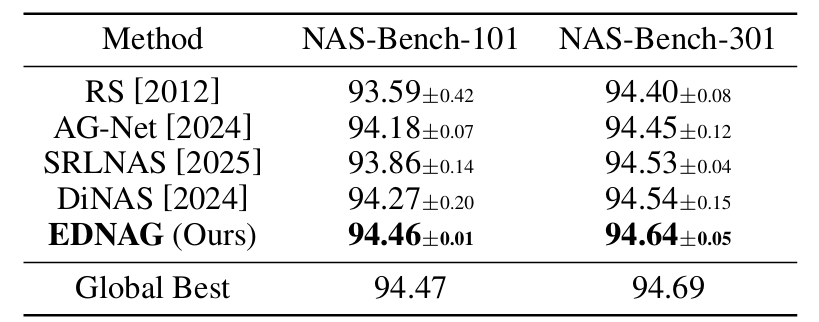
NAS-Bench-101 & NAS-Bench-301

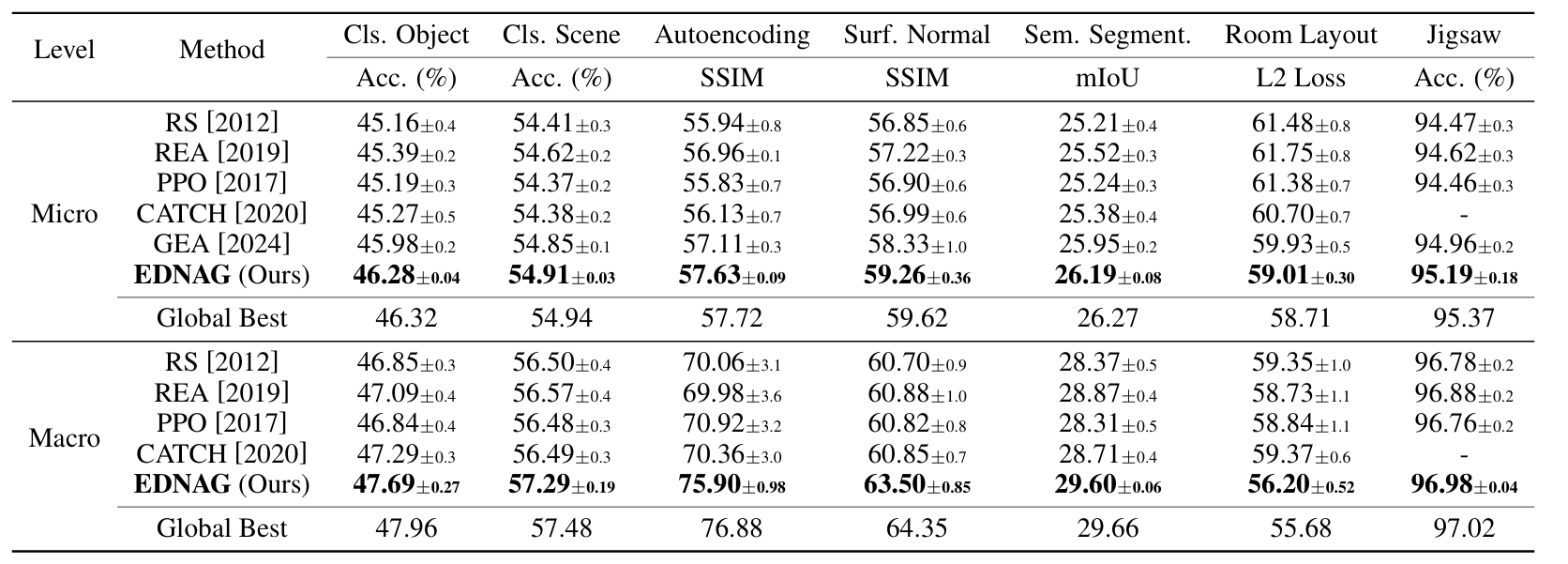
NAS-Bench-201

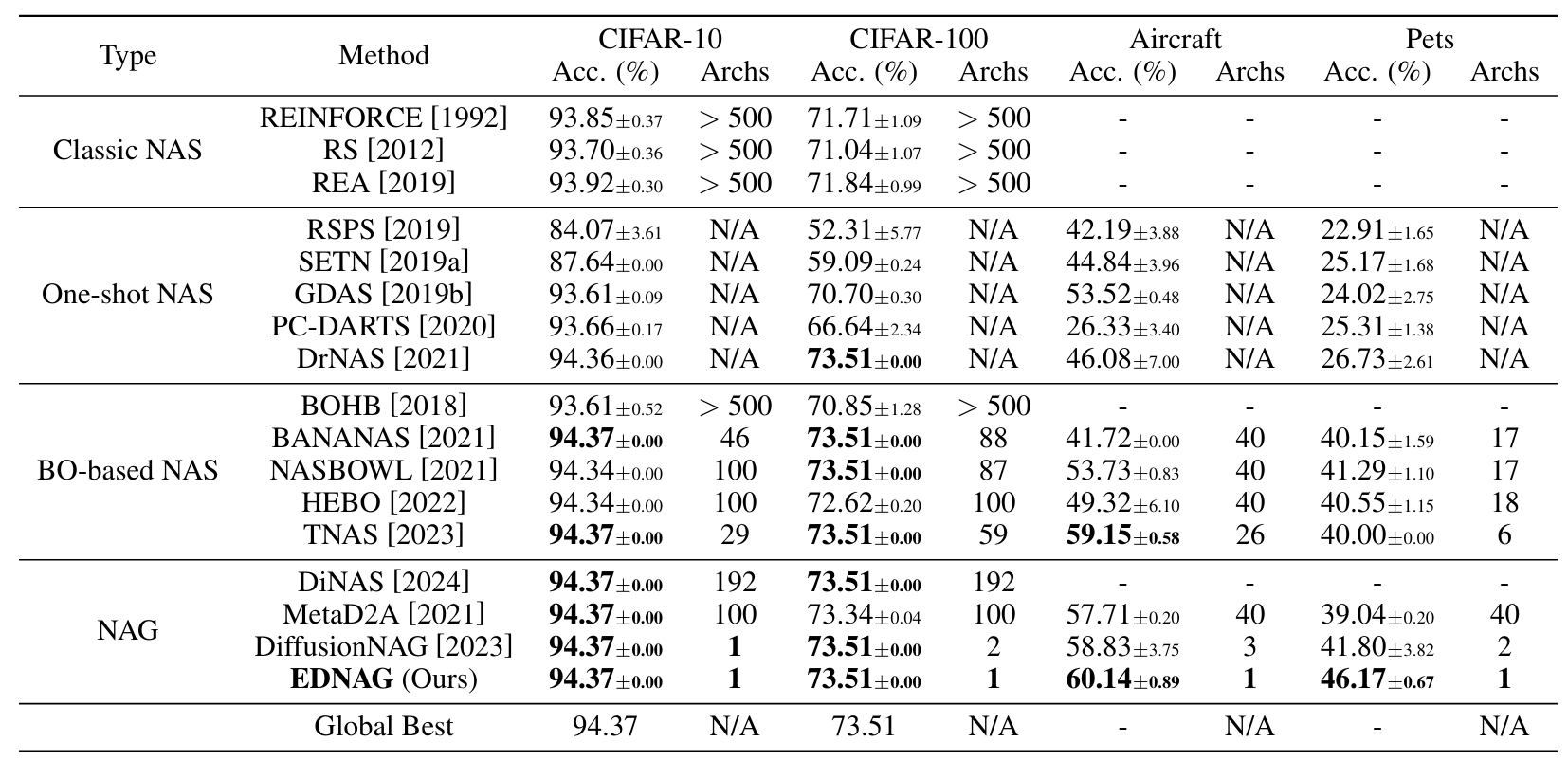
TransNASBench-101

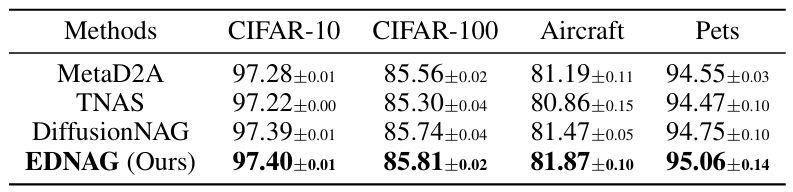
MobileNetV3

GPU Time Costs

NOAA Fisheries Steller Sea Lion Population Count

Introduction

We tackle the challenge of automated Steller sea lion population counting from aerial imagery—a task critical for ecological monitoring but complicated by dense crowds, occlusions, and varying object scales. Existing detection and segmentation methods often falter in this domain due to frequent overlaps and annotation inconsistencies. In this work, we introduce YouCount, a robust YOLOv11-based pipeline enhanced by a novel Adaptive Bounding Box Coordinates Annotation Framework (ABC). Our method adaptively refines bounding boxes and utilizes dual patch generation strategies to effectively capture dense and overlapping instances. Extensive experiments on the NOAA Fisheries Steller Sea Lion Population Count dataset demonstrate the superiority of our approach, achieving an RMSE of 11.65312 and earning 2nd place in the corresponding Kaggle competition. Ablation studies further validate the effectiveness of our adaptive annotation and training strategies.

Why Counting Steller Sea Lions?

• Population Crisis:
  Steller sea lion numbers have drastically declined in the western Aleutian Islands.
  Conservation efforts are urgent and require accurate population data.
• Challenges in Manual Counting:
  Requires highly trained personnel.
  Time-sensitive and resource-intensive.
• Significance of Accurate Estimates:
  Critical for understanding population dynamics.
  Informs and improves conservation strategies.
  Helps identify recovery barriers in specific regions.

Contributions

• Introduce YouCount: a YOLO11-based counting method.
• Propose ABC Framework: improves annotation with adaptive bounding boxes.
• Achieved 2nd runner up in Kaggle competition, RMSE: 11.65.

Related Works

Object Detection methods (e.g., Fast-RCNN, ResNet) provide bounding boxes with confidence scores and perform well in moderately dense scenes, but struggle with bounding box confusion in crowded images and are sensitive to scale and perspective changes. Instance Segmentation methods (e.g., UNet) offer improved handling of overlapping objects and more accurate shape modeling via masks, yet are prone to errors from posture variation and segmentation instability, which impact counting accuracy.
In the NOAA dataset, sea lion categories are annotated with colored dots, typically converted into fixed-radius circles (for segmentation) or fixed-size squares (for detection). However, these traditional annotation strategies have key limitations: they enforce size uniformity, ignoring natural variations in sea lion size; they create shape mismatches, as sea lions are not perfectly circular or square; and, in dense clusters, overlapping annotations lead to ambiguity and confusion during model training.

Methods

Adaptive Bounding Box (ABC)

• Adaptive Bounding Box Generation:
  • Start with square bboxes centered on annotated dots.
  • Resize using IoU-based scaling & distance-aware directionality.
  • Prevent overly small boxes with min-size constraint.
• Patch Extraction Strategies:
  • Overfitting-Based Patching:
    • Randomly samples bbox-centered patches (30% of total).
    • Limits number of patches per image (1–3).
  • Tiling-Based Patching:
    • Slides a fixed-size window (stride = 95%) over image grid.
    • Enables dense coverage with overlap.
• Patch Filtering:
  • Discard clipped bboxes (<20% original area).
  • Discard patches with >50% black pixels.
  • Downscale all valid patches from 1280 to 640 for YOLO input.

YOLO-Based Counting (YouCount)

• Training Phase:
  • Input: annotated patches with bounding boxes and class labels.
  • Model: YOLO11 with multi-scale detection.
  • Techniques: heavy data augmentation and learning rate scheduling.
• Inference Phase:
  • Resize patches to 640×640 for YOLO.
  • Predict bounding boxes and class probabilities.
  • Apply Non-Maximum Suppression (NMS) to remove overlaps.
• Count Refinement:
  • Edge-weighting rule:
  • Near 1 edge → ×0.7
  • Near 2+ edges → ×0.5
  • Reduces double-counting from overlapping patches.
• Post-Processing:
  • Apply category-wise scaling based on bias correction:
  • Pups ×1.3, Juveniles ×0.85, Adult Females ×0.96
  • Adult Males ×1.55, Subadult Males ×1.2

Experiments

Public test RMSE: 11.68482
Private test RMSE: 11.63121

In-depth Analysis

Acceleration and Deployment of Large Language Models

Introduction

LLM-Acceleration is an open-source project focused on optimizing the Llama-3.2-3B-Instruct language model to achieve faster and more memory-efficient inference while preserving model quality, enabling advanced large language models to run on consumer hardware. The project integrates several state-of-the-art techniques, including QLoRA fine-tuning, 4-bit GPTQ quantization, and the VLLM inference engine with further enhancements such as 8-bit KV-cache and speculative decoding. By combining these methods, the pipeline significantly reduces computational and memory requirements, making it possible to deploy powerful language models locally on a wide range of devices, from mainstream GPUs to more modest hardware. We further efficiently deployed large language models like Llama-3.2-3B-Instruct on everyday consumer hardware—including both discrete and integrated GPUs—enabling powerful, private, and cost-effective AI applications to run locally in web browsers without the need for expensive cloud infrastructure.

Contributions

• Memory-efficient finetune with QLoRA, and then qauntize with AutoGPTQ for W4A16.
• Infer with VLLM inference engine, CUDA graph compilation, quantized 8-bit KV-Cache, and speculative decoding.
• Deploy to a browser-based AI chatbot with WebLLM, which runs LLama-3.2-3B-Instruct entirely on the user side using WebGPU withconsiderable throughput.

Acceleration

The optimization pipeline consists of three main stages.

• QLoRA Fine-tuning: Fine-tunes Llama-3.2-3B-Instruct with QLoRA using 4-bit quantization, low-rank adaptation, and gradient checkpointing, greatly reducing memory and trainable parameters; model is saved as Llama3.2-3B-Instruct-QLoRA-finetuned.
• GPTQ Quantization: Applies 4-bit GPTQ quantization to both the fine-tuned 3B model and base 1B model, using calibration samples for accuracy, resulting in Llama3.2-3B-Instruct-quantized and Llama-3.2-1B-Instruct-GPTQ-Quant.
• VLLM Inference with Advanced Optimizations: Runs inference using VLLM with Xformers, 8-bit KV-cache, speculative decoding, chunked prefill, prefix caching, and kernel compilation, enabling efficient large-scale inference with reduced memory and achieving PPL 11.22 and 80.36 tokens/sec throughput on T4 GPU.

The optimized pipeline achieves excellent performance metrics on T4 GPU in Colab:
Perplexity (PPL): 11.217229843139648 (on WikiText-2-raw-v1 test set)
Throughput: 80.36136051159993 tokens/second

Deployment

We leverage WebLLM to run language models directly in the browser with WebGPU.

We deployed the quantized model on NVIDIA RTX 3060 GPU in laptop, as shown in this video. The NVIDIA GeForce RTX 3060, built on the Ampere architecture with a GA106 core, features 3584 CUDA cores, a boost clock of 1777 MHz, 6GB VRAM memory, supports DLSS 2.0 and second-gen ray tracing, and delivers strong 1080p and 1440p gaming performance while maintaining a 170W TDP. On this GPU, the model can run with a throughput of 25.1744 tokens per second.

Moreover, we deploy the quantized model on AMD 7840H in laptop. The AMD Ryzen 7 7840H features an integrated GPU known as the Radeon 780M, which features RDNA 3 architecture with 12 Compute Units (768 stream processors), and supports DirectX 12 Ultimate, Vulkan, and basic ray tracing. Notably, the Radeon 780M integrated GPU in the AMD 7840H does not have dedicated VRAM but dynamically shares system memory (RAM), with allocation varying based on BIOS settings, OS management, and the installed RAM type and capacity. On this GPU, the model can run with a throughput of 11.1195 tokens per second.

SCU-ACM-OJ

Introduction

SCU-ACM-OJ is an Online Judge system specifically designed for school-level ACM programming competitions, aimed at addressing the issues of existing OJ systems being unsuitable for school-level competitions. The system significantly enhances competition organization efficiency and participants' experience through a simple user interface, efficient competition organization, and comprehensive evaluation and feedback.
SCU-ACM-OJ is the first OJ system developed specifically for school-level ACM competitions. It provides administrators with automated file parsing to facilitate bulk competition registration and problem package uploads. Additionally, it features a code security detection mechanism based on LLM, offering comprehensive functional support, efficient competition management, and a secure and reliable platform for school-level ACM competitions.

Related Projects

• Feature Mismatch
  • The functionality of some platforms is either too complex or too simple, failing to meet the requirements of university-level ACM competitions.
  • C Language Online provides only a basic user interface and minimal features.
  • Luogu offers many redundant modules, such as practice, simulation, community, and competitions, making it unsuitable for campus contests.
  • LeetCode employs a core code evaluation mode that differs from ACM standards, which is not conducive to ACM-style events.
• Architectural and Scalability Issues
  • Monolithic architectures result in tightly coupled modules, hindering flexibility.
  • HUSTOJ’s judge logic directly interacts with MySQL tables, causing strong dependencies and blocking horizontal scaling.
  • BOJ tightly couples code evaluation with auxiliary functions; high traffic in the judging queue can bring down the whole service.
  • TOJ requires static server allocation for competitions and cannot be distributed, leading to over 60% resource idleness when idle.
• Security and Isolation Limitations
  • Overall system security and evaluation environment isolation are insufficient.
  • RQNOJ relies on a traditional C-language sandbox, unable to detect supply chain risks from Python third-party libraries.
  • Vijos uses a complex C-language sandbox; inadequate isolation has previously allowed user code to attack the host server via ptrace.

Implemented Features

Competition List Navigation: Users can view the competitions they have registered for here.

Competition Details: View the submission and evaluation status for each problem in the current competition.

Browsing Problems and Code Evaluation:
Users can view the time and memory limits for each problem and download the problem statements here.
Users select an evaluation template, submit their solution code, and finally check the evaluation results.

Competition Leaderboard: Users can view the competition leaderboard. During the competition, the real-time submission status of each participating team will be displayed.

User Login: Two login methods are supported—account and password, or email and verification code.

Add New Problem:
Set problem description
Set memory limit
Set time limit
Upload problem archive
The problem archive can be downloaded from the Polygon shared problem setting platform!

Competition Creation and Registration:
Set competition description
Set start and end time
Select user list (or upload an Excel file directly)
Select competition problems

User Management: Modify username, password, and email.

Technical Features

Microservices Architecture:
Each service is decoupled from the others, so a failure in one service has minimal impact on the rest.
Each service is highly scalable, making system integration of new services easier.
Each service is deployed independently, allowing for efficient allocation of servers with different performance levels and improving resource utilization.

User Authentication:
1. Role-based access control: user, admin, and super admin.
2. Login expires after 6 hours and requires re-authentication.
3. When permissions are invalid or the session has expired, users cannot navigate to pages or perform operations.

Multi-language Judging System:
1. Supports Java, C & C++, and Python code.
2. Plug-and-play design with high scalability and versatility!
3. Calculates code runtime and memory usage via system calls.

High-Concurrency Judging Support:
1. Judging code uses asynchronous communication to avoid blocking the main thread and prevent user lag during evaluation.
2. Message queues are used to handle high-concurrency judging demands.
The submission time for judging is recorded when the request enters the judging queue.

Malicious Code Defense:
1. Malicious code detection model based on GLM-4-AIR.
2. Fully leverages the powerful generalization and code analysis capabilities of large language models (LLMs) to achieve more comprehensive security detection.
3. Docker-based virtual environment.
4. Even if malicious code is missed, it will not cause significant harm to the system!
5. Restoring the judging service only requires copying the initial container, which is very fast and simple!